Let's explore a different direction. At 0.001 seconds per random number, computation time is about 10x the packet latency; the program is still processor bound and hence likely to scale well. What if we shift the delay down to 0.0001 seconds per random number but generate ten times as many random numbers (so it should run in about the same amount of time?
$ random_pvm_master -d 100000 -n 1 -r 100000
1 100000 100000 13.8996855957
This is a reasonable number, although it is a bit longer than we expect. Something is not quite right. Let's shoot for two nodes:
$ random_pvm_master -d 100000 -n 2 -r 100000
2 100000 100000 30.9584868153
Whoa! This took longer than one node. A lot longer. We can understand why. We had to send 100,000 messages over the network (instead of 5000). Each message had a latency of perhaps 200 microseconds, so 100,000 of them take about twenty seconds to send. In addition, it takes around 10 seconds to "compute" the 100,000 rands at 100 microseconds each. Total: 30 seconds.
Things are really even more complex than this indicates when running on more than two nodes. For example, consider:
$ random_pvm_master -d 100000 -n 3 -r 100000
3 100000 100000 105.5901358108
96.110user 1.730sys 92.6%, 0ib 0ob 0tx 0da 0to 0swp 1:45.60
$ random_pvm_master -d 100000 -n 4 -r 100000
4 100000 100000 17.1603190026
Clearly something evil and nonlinear is happening where some of the node messages are considerably delayed and things are less predictable than one would like. Latency bound parallel computations are notorious for being sensitive to state -- things like the order of the communications and how busy the network is start to really matter. My test network isn't the quietest one in the world, but neither is it so noisy that such wide variations in runtime would occur if the network weren't jammed.
However, we can make our difficulties magically go away. Let's try the -b flag, and send ALL the random numbers generated by each host in single messages, which the network stack will then efficiently break up into large packets and send at a rate limited by bandwidth, not latency. All 400,000-odd bytes requested by the master should take a bit less than 0.5 seconds to send, not twenty or more, and poof!
$ random_pvm_master -b -d 100000 -n 4 -r 100000
4 100000 100000 2.6034640411
Nearly perfect scaling relative to a ten second base computation time is restored!
These results are not all that random_pvm has to teach us, not by a long shot, but it is enough for now. As an exercise, use your cluster to explore various ranges of delay, number of slaves, and number of rands, with and without aggregation of the communications. You should be able to generate pretty graphs, and those graphs should be readily understandable on the basis of our earlier discussions of Amdahl's Law.
If nothing else, you should get the following out of this month's column:
- Computation time > Communication Time is Good (for speedup/scaling).
- Computation time <Communication Time is Bad.
- Aggregating communications is one very important way of shifting a task from communication bound (bad) back to computation bound (good).
That and a working example of a Real Parallel Program written with PVM, that is. Not too shabby.
And Now For a Bit of Fun...
To wrap up this month's column, let's run one more trivial example but look at it using XPVM (the pretty PVM GUI):
$ random_pvm_master -d 100000000 -n 6 -r 100; \
sleep 1; \
random_pvm_master -b -d 100000000 -n 6 -r 100
6 100 100000000 1.7201111265
6 100 100000000 1.7161686264
The first of these generates a run of only 100 random numbers from six hosts (but with a 0.1 second delay in between), sending each number back to the master is it is generated. The second does the same with aggregation. The sleep in between is to separate the two runs in the XPVM trace.
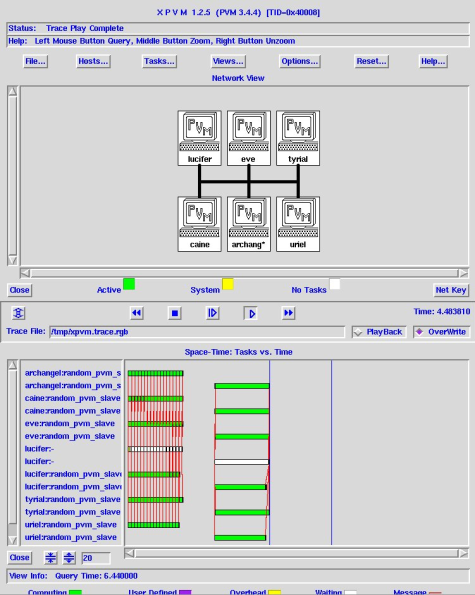
Examine the traces of these two tasks on your cluster with XPVM (see e.g. Figure One) and you will note that the first job is represented by six very busy green bars (the slave tasks) each talking to the mostly idle white bar (the master task) with the communications represented by lots of little red threads. Remember, the red threads are fun but "bad" from the point of view of scaling.
The second job is also six green bars for the six slaves working full time, a truly thumb-twiddling idle white master, and just one red thread at the end where the results are shot back. At this (computation bound) scale, there is no meaningful difference in runtime, but imagine the dense forest of red that would result on this timescale if we were sending back thousands of rands per second from each of the nodes. Eventually it literally saturates the ability of the network to keep up and the task is liberally and somewhat unpredictably delayed.
That's it for this month. At this point you are ready to become a real parallel programmer; random_pvm can easily be hacked into all sorts of master/slave parallel tasks both useful and just for fun. In future columns we may return to PVM and consider other programming models -- and maybe even more PVM commands!
| Sidebar Two: PVM Resources |
|
PVM Home Page
PVM Users Guide PVM: A User's Guide and Tutorial for Networked Parallel Computing, Geist, Beguelin, Dongarra, Jiang, Manchek and Sunderam (MIT press)
|
This article was originally published in ClusterWorld Magazine. It has been updated and formatted for the web. If you want to read more about HPC clusters and Linux, you may wish to visit Linux Magazine.
Robert Brown, Ph.D, is has written extensively about Linux clusters. You can find his work and much more on his home page


