A step by step guide
It is a common practice to have development and test servers for each production server, so that you can experiment with changes without the fear of breaking anything important, but this is usually not feasible with clusters. So how do you try that new version of your favorite program before committing it to the production cluster? A cheap and convenient possibility is to build a virtual cluster.
Thanks to the Xen virtual machine monitor, you can create a number of virtual machines, all running simultaneously in your computer, install different operating systems in them, or just different configurations, and connect them via (virtual) network cards. Xen is a terrific tool for building virtual Beowulf clusters. It can prove useful when learning or teaching about clusters or for testing new features/software without the fear of causing major damage to an existing cluster.
This guide is the first of a series in which I give you detailed step-by-step instructions on how to build a virtual cluster with Xen. The cluster thus built might not be appropriate for your case, and does reflect the author's preferences and/or needs, but if you are new to clusters or Xen, it will hopefully help you get started with both.
The goal is to start it simple and then add more complexity as we progress, so in this first guide I show you how to get do the basics:
- A Xen installation, the creation of 5 virtual machines (one to act as the master and four slaves),
- Shared storage through NFS,
- The network configuration on which to build the virtual cluster.
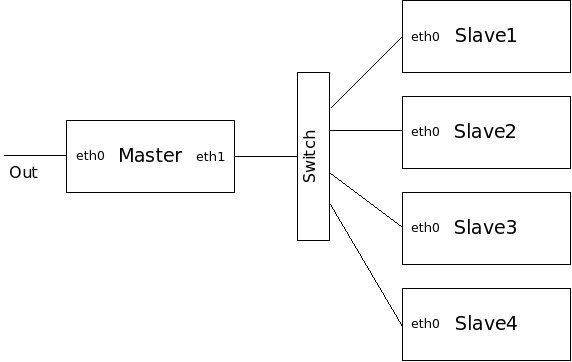
The network structure of this first attempt will be very simple, the master having two network cards, one to the outside world and the other one connected through a switch to the slaves. The virtual cluster is shown below in Figure One.
Xen Installation
In this section, we will do the basic work to get our virtual cluster ready, by installing Xen. As per the remainder of the guide, if you are an experienced user, you might want to deviate from the steps provided here, although then you may have to solve a number of problems if they arise. If you have no such experience, I would suggest you to follow this guide as close as possible the first time, and later redo your cluster if you wish. Furthermore, to make sure that you can follow the steps precisely, you would need a computer ready to be wiped clean (i.e. a sandbox system). In addition, it is assumed that you will be able to get appropriate necessary IP addresses and names for you system. (one for the host computer and another one for the master node of the cluster).Let's start with a fresh install of the operating system in a moderately powerful computer (in my case a Dell Optiplex GX 280 with 1GB of RAM and a 150GB disk). As configured here, the master needs 128MB of RAM and each slave 64MB, so if you wanted to configure many more slaves, you should probably get more RAM. Disk space is not an issue, as the master requires roughly 2GB and each slave 1GB (to a grand total of 6GB). In this guide we assume a Ubuntu version 5.10 system. In principle Xen would work with any other distribution, but Ubuntu has become really popular lately, and it provides a very simple install, requiring only one CD, which you can download from one of the Ubuntu mirros (5.10 is not the most current version, however).
For my Dell Optiplex GX 280, I downloaded one ISO file, burned it and installed Ubuntu from it. The installation of Ubuntu is truly simple and the only relevant things to mention are: We don't want bells and whistles for our host machine, so when asked, type "server" to perform a server installation. In our case the host machine is called "yepes" and the user account "angelv" When asked about partitions we selected to ERASE THE ENTIRE DISK Assuming you have a DHCP server at your place, the network will be automatically configured to use it.
Shortly you should have Ubuntu installed in your machine. Bear in mind that in Ubuntu there is no root account as default, so all the privileged commands are executed with the "sudo" command with the user account just created ("angelv" in my case). As shown below, we will need to install some extra packages which are needed for Xen (see the Xen manual), and for convenience, we will change the network configuration to use a static IP address.
angelv@yepes:~$ sudo aptitude install openssh-server emacs21 lynx bridge-utils make patch gcc zlib1g-dev libncurses5-dev libncursesw5-dev python2.4-dev
In order to change the network configuration, we will need to modify the file /etc/network/interfaces and replace the line "iface eth0 inet dhcp" with something like (obviously you should find the correct values for your institution):
iface eth0 inet static address 161.XX.XX.XX netmask 255.XX.XX.XX gateway 161.XX.XX.XX
DNS configuration is probably properly configured already, but check the file /etc/resolv.conf. Restart the network (with commands: sudo ifdown eth0 and sudo ifup eth0), and verify that everything is correct (you can use the command ifconfig and use the text-based web browser lynx to verify that you can access the Internet).
We are now ready to download Xen, compile it (which will take quite a while) and install it, which we will do from the source code. Since we don't have latex installed, the documentation will not be created, and since we will need NFS server support in the master node, we will need to recompile the kernel for the virtual machines (for info on kernel recompilation see Kernel Building HOWTO). To accomplish this, we do the following:
angelv@yepes:~$ wget -nd http://www.cl.cam.ac.uk/Research/SRG/netos/xen/downloads/xen-3.0.1-src.tgz angelv@yepes:~$ tar -zxf xen-3.0.1-src.tgz angelv@yepes:~$ cd xen-3.0.1 angelv@yepes:~/xen-3.0.1$ make world angelv@yepes:~/xen-3.0.1$ cd linux-2.6.12-xenU/ angelv@yepes:~/xen-3.0.1$ make ARCH=xen menuconfig
We activate the options for NFS Server Support (and NFS V3 server support inside it) in the menu File Systems -> Network File Systems. Then, after saving the configuration changes, we do the recompilation and the installation:
angelv@yepes:~/xen-3.0.1$ cd .. angelv@yepes:~/xen-3.0.1$ make angelv@yepes:~/xen-3.0.1$ sudo make install
Once the installation is complete, we will have to modify the boot loader, so that it takes the new kernel as default. For this, we modify the file /boot/grub/menu.lst adding the following as the first entry to the kernels, i.e. right after the line "## ## End Default Options ##" (NOTES: the root device /dev/sda1 might be /dev/hda1 in your case. Just look at the other kernel entries in your menu.lst to find the right option. The max_loop option is to generate more loops, which is necessary in our case, since we need to create 5 machines):
title Xen 3.0 / XenLinux 2.6 kernel /boot/xen-3.0.gz dom0_mem=262144 module /boot/vmlinuz-2.6-xen0 root=/dev/sda1 ro console=tty0 max_loop=32
The next step will make sure that Xen starts automatically and will eliminate the Local Thread Storage (TLS) library, which gives problems to Xen (see section 2.5.3 of the manual). Enter the following:
angelv@yepes:~/xen-3.0.1$ sudo update-rc.d xend defaults angelv@yepes:~/xen-3.0.1$ sudo update-rc.d xendomains defaults angelv@yepes:~/xen-3.0.1$ sudo mv /lib/tls /lib/tls.disabled
You can now reboot the machine, and verify that it boots into the Xen kernel, and check that Xen is running correctly by running the command sudo xm list, which should show that Domain-0 is the only machine at the moment.
Creation of Virtual Machines
An unmodified operating system cannot be installed in a Xen virtual machine (unless we use some of the modern processors with VT technology), but in order to avoid having to modify the operating system ourselves, we can use one of the OS already prepared for Xen at Jailtime.org. For our virtual cluster we are going to install CentOS, which can be downloaded using the previously installed lynx browser to obtain the file centos.4-3.20060325.img.tgz from Jailtime.org. Next, we will have to create directories to hold the OS images for each of the machines of our virtual cluster:angelv@yepes:~$ tar -zxf centos.4-3.20060325.img.tgz angelv@yepes:~$ sudo mkdir -p /opt/xen/cray/master (repeat for slave1-4) angelv@yepes:~$ sudo cp centos.swap /opt/xen/cray/master/ angelv@yepes:~$ sudo cp centos.4-3.img centos.swap /opt/xen/cray/slave1/ (repeat for slave2-4)
The image thus created is 1GB, which should be sufficient for the slaves, but not for the master, since we will want to install more things in it, plus it will work as NFS server, so we have to resize the centos.4-3.img for the master:
angelv@yepes:~$ dd if=/dev/zero of=/tmp/zero.xen bs=1M count="1024" angelv@yepes:/etc/xen/boldo-jaguar$ sudo e2fsck -f centos.4-3.img angelv@yepes:/etc/xen/boldo-jaguar$ cat centos.4-3.img /tmp/zero.xen >> centos.4-3.2GB.img angelv@yepes:/etc/xen/boldo-jaguar$ resize2fs centos.4-3.2GB.img angelv@yepes:/etc/xen/boldo-jaguar$ e2fsck -f centos.4-3.2GB.img angelv@yepes:/etc/xen/boldo-jaguar$ sudo cp centos.4-3.2GB.img /opt/xen/cray/master/centos-4-3.img
The next step is to create the configuration files for each of the virtual machines. For this, we will create the directory to hold them, sudo mkdir -p /etc/xen/cray, and will create inside it the file master.cfg, slave1.cfg, slave2.cfg, slave3.cfg and slave4.cfg. The contents of master.cfg should be:
kernel = "/boot/vmlinuz-2.6-xenU" memory = 128 name = "master" vif = [ '', ''] disk = ['file:/opt/xen/cray/master/centos.4-3.img,sda1,w','file:/opt/xen/cra/master/centos.swap,sda2,w'] root = "/dev/sda1 ro"
The contents of slave1.cfg should be as follows (the contents of the other slaves.cfg are the same, but replacing slave1 for the corresponding name):
kernel = "/boot/vmlinuz-2.6-xenU" memory = 64 vcpus = 4 name = "slave1" vif = [ '' ] disk = ['file:/opt/xen/cray/slave1/centos.4-3.img,sda1,w','file:/opt/xen/cray/slave1/centos.swap,sda2,w'] root = "/dev/sda1 ro"
Note that the entry vif for the master has two values, which will configure it as a machine with two network cards, and the entry vcpus for the slaves has the value 4, which will configure them as SMP nodes with four processors each.
Cluster Network Configuration
With the steps performed until now, we would be ready to start all the five machines, but we will need to modify the default network settings. We could either do this by booting the machines and performing the changes on a live system, or better by modifying the images before booting it. Let's first configure the master node.
Master Configuration:
You can modify any file in the OS image by mounting it with the loop option like this:
angelv@yepes:~$ mkdir tmp_img angelv@yepes:~$ sudo mount -o loop /opt/xen/cray/master/centos.4-3.img tmp_img/ angelv@yepes:~$ sudo emacs /home/angelv/tmp_img/etc/sysconfig/network
With this method we will modify the necessary files for the network configuration (ifcfg-eth0, ifcfg-eth1, network and resolv.conf) with the following contents:
angelv@yepes:~$ cat tmp_img/etc/sysconfig/network NETWORKING=yes HOSTNAME=boldo GATEWAY=161.XX.XX.XX angelv@yepes:~$ cat tmp_img/etc/resolv.conf search ll.iac.es iac.es nameserver 161.XX.XX.XX nameserver 161.XX.XX.XX angelv@yepes:~$ cat tmp_img/etc/sysconfig/network-scripts/ifcfg-eth0 TYPE=Ethernet DEVICE=eth0 BOOTPROTO=static IPADDR=161.XX.XX.XX NETMASK=255.XX.XX.XX ONBOOT=yes angelv@yepes:~$ cat tmp_img/etc/sysconfig/network-scripts/ifcfg-eth1 TYPE=Ethernet DEVICE=eth1 BOOTPROTO=none IPADDR=192.168.1.10 NETMASK=255.255.255.0 ONBOOT=yes USERCTL=no PEERDNS=no NETWORK=192.168.1.0 BROADCAST=192.168.1.255 angelv@yepes:~$
Note that in our case we named the master node as boldo, with two network cards, eth0 with a static IP address which should be provided to you at your institution and eth1 with IP 192.168.1.10 in a private network. The values for Gateway, Netmask and DNS server are dependent on your network. In our case we put the same as for the host machine yepes, so that the master node of the cluster is like any other machine in our network. Once we have done this we unmount the OS image with the command sudo umount tmp_img/ After doing these changes, we start the master node with the following command and verify that the network is working correctly:
angelv@yepes:~$ sudo xm create -c /etc/xen/master.cfg
As stated at Jailtime.org the root password is password. Obviously you should change it right now. Check that the values for the network cards are correct with the command ifconfig Verify that you have network connectivity (for example by doing wget -nd http://www.google.com) Once inside a virtual machine, we can disconnect by typing Ctrl-] To reconnect to the virtual machine from the host machine, we can use the command sudo xm console master (the name provided in the configuration file). You will have to press the return key to obtain the prompt.


