Taskmaster and its Task
With this as motivation, let us return to running taskmaster on our NOW. The command syntax for taskmaster is:taskmaster hostfile nhosts nrands delay
where nhosts is the number of hosts to use (less than or equal to all of the hosts in hostfile), nrands is the number of random numbers you wish it to generate, and delay is the delay, in seconds, between each random number returned by each host.
With the list of ssh-accessible cluster nodes in hostfile, enter the following sequence of taskmaster jobs and record the return time for each. The example assumes that you have at least 8 hosts in hostfile; if not, use the biggest number of hosts you do have.
$ taskmaster hostfile 8 40 1 q > scaling.8 $ taskmaster hostfile 8 40 2 q >> scaling.8 $ taskmaster hostfile 8 40 3 q >> scaling.8 $ taskmaster hostfile 8 40 4 q >> scaling.8 $ taskmaster hostfile 8 40 5 q >> scaling.8 $ taskmaster hostfile 8 40 10 q >> scaling.8 $ taskmaster hostfile 8 40 20 q >> scaling.8
With an editor and a calculator compute and edit in the parallel efficiency = (nrands*delay)/(nhosts*time). A typical result might look like (also plotted in Figure One):
# nhosts nrands delay time parallel efficiency(%)
8 40 0 3 0
8 40 1 7 71
8 40 2 12 83
8 40 3 17 88
8 40 4 22 91
8 40 5 27 93
8 40 10 52 96
8 40 20 101 99
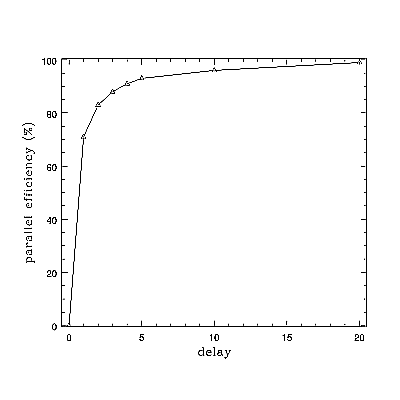
Let us understand this. We are generating 40 random numbers on 8 hosts,or five random numbers apiece. If delay is 0, it takes about 3 seconds just to start up the remote jobs and get back their (nearly instantaneous) replies with the results. However, it would take only 40*0 = 0 seconds (rounded) to generate all 40 on a single host, so efficiency is terrible.
If it takes 1 second per random number per host, the overhead of starting up and getting back the results actually goes down a bit, as the first hosts started up get to do some work while the rest of them start up and so less time is lost. It would take a single host 40 seconds to generate 40 rands (nrands*delay). A perfect speedup with 8 hosts would be 40/8 or 5 seconds total to generate our five rands. It takes us 7, so our efficiency is 5/7 or around 71%. And so on.
The important thing to learn from this is that as the work done to generate another rand (simulated by delay) increases relative to fixed overhead starting up the jobs and sending the rands back to taskmaster, the efficiency increases as well, approaching 100% as the work done takes much much longer than the startup and communication times! This is a scaling rule -- a rule that tells us what sort of parallel speedup to expect.
Let's extract and look at another. Following the general formula above and with calculator and editor in hand, use taskmaster and task to generate the following sequence of results:
| nhosts | nrands | delay | time | speed=nrands/time |
|---|---|---|---|---|
| 0-8 | 8 | 1 | ? | ? |
| 0-8 | 16 | 1 | ? | ? |
| 0-8 | 24 | 1 | ? | ? |
| 0-8 | 40 | 5 | ? | ? |
The results should look approximately like Figure Two, where [open triangles] are nrands=8, [open squares] are 16, [open pentagrams] are 24, and [filled triangles] are 40 with a delay of 5 instead of 1. The dashed line is perfect speedup - using N nodes makes the fixed size job complete in 1/N of the time, for an N-fold speedup.
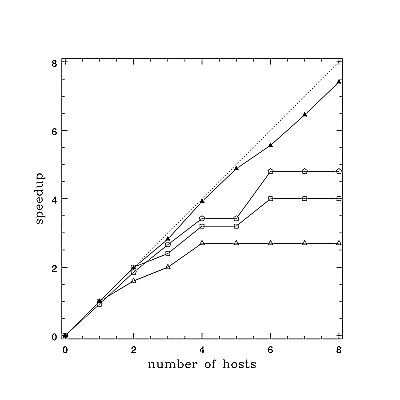
Figure Two is a very informative figure. It illustrates many of the basic principles of cluster design and task scaling. From it we see that when a task is divided up among nodes in such a way that each node does a small amount of a small increment of work (compared to the overhead of task startup and communication) we may not speed up much as we increase the number of nodes allotted to the task. In the first three cases, we stopped speeding up altogether when between four and six nodes were assigned to the task (and have the uncomfortable, and correct, feeling that in the general case adding too many nodes could make the task slow down). However, we could assign more nodes to the task with some speedup resulting as we increased the amount of work being split up. Increasing the number of rands being generated helped some, but what really helped was increasing delay, the amount of "work" being done per rand. As we saw in Figure One, making delay large pushed the parallel speedup to one.
Conclusion
Hopefully it is becoming apparent that cluster design requires a pretty good understanding of the scaling rules we observe in the figures above. Clearly we have identified a couple of "knobs" that can make a given cluster design more -- or less -- efficient, but they aren't in the hardware at all, they are in software! Or rather (no be more fair) they are linked to the hardware characteristics that determine things like the time required to complete an assigned work increment on a node. Still, if we had to summarize the results of today's exercises in a single phrase, it would be something like: coarse grained, gooood, fine grained, baaaaad. That's easy enough to remember.There are a few other important "knobs" that remain to be discovered. Some of these knobs are very much in hardware (for example, the speed of the network). Next month we'll tackle an important piece of algebra connected to a scaling relation known as Amdahl's Law. Using what we have learned so far, we'll derive an equation that describes the two figures above quite well (within the jigs and jags caused by using just a single sample with a fairly course time unit). With this equation in hand (and some measurements and thought) we can start to get a pretty good idea of the kind of performance we can expect from a given kind of cluster built for a given kind of problem -- before we spend all that money building the wrong kind (defined as one that wastes your money -and/or fails to get your work done).
This article was originally published in ClusterWorld Magazine. It has been updated and formated for the web. If you want to read more about HPC clusters and Linux, you may wish to visit Linux Magazine.
Robert Brown, Ph.D, is has written extensively about Linux clusters. You can find his work and much more on his home page


