In our previous installment, we started out by learning how to use pretty much an arbitrary Linux LAN as the simplest sort of parallel compute cluster. In this column we continue our hands-on approach to learning about clusters and play with our archetypical parallel task on our starter cluster to learn when it runs efficiently and just as important, when it runs inefficiently.
If you've been following along, in last column we introduced cluster computing for the utter neophyte by "discovering" that nearly any Linux LAN can function as a cluster and do work in parallel. Following a few very general instructions, you were hopefully able to assemble (or realize that you already owned) a NOW (Network of Workstations) cluster, which is little more than a collection of unixoid workstations on a switched local area network (LAN). Using this cluster you ran a Genuine Parallel Task (tm).
If you missed the last issue, to participate in this month's column fully you should try to find or assemble a Linux/UNIX (but I will always assume Linux in this column as it is what I use at home and work) LAN so that you have account space on all the workstations (a.k.a. "nodes" in the context of cluster computing). Each node should have ssh set up so that you can login to it from your personal workstation (the "head node") using ssh without a password (following instructions in the man pages and other on-line documentation).
Beyond a fairly generic Linux workstation installation on each node, you'll need to make sure that the head node has a recent version of perl (one that supports threads) as well as gcc and make, and you'll need to download the source code from last month's for "taskmaster" (a threaded "master" application that initiates a task on many hosts in parallel and collects the results) and "task.c" (the task). This code has a tiny change (in taskmaster) relative to last month's source that makes the output less verbose when all you are doing is using it to do timings.
The task itself is a work assignment for a node that loops over a sleep for a delay passed to it by the taskmaster, then generates a random number (uniform deviates in the range 0.0-1.0) and returns it to the originating taskmaster thread, until nwork random numbers have been returned. The value of delay represents the amount of simulated work that has to be done by the node to return a number. This will turn out to be an important number, and this column is largely about exploring the various limits of behavior that one can see for different ratios of work done (delay) to the presumed fixed time required by each node to send its number back to taskmaster for assembly and presentation.
To get set up to play, perform the following tasks:
- Put the code for task.c and its Makefile in a subdirectory on your personal or primary system(s) and build it (just entering "make" should do it, if gcc and make are installed and correctly set up).
- Put the resulting "task" binary on a consistent path on all the systems that will participate (with e.g. cp or scp). This might be someplace like $HOME/bin/task or /tmp/task. I'm assuming the latter in the taskmaster script below or you can edit taskmaster and put it where ever you like. You can execute task without arguments to see its argument list, and should execute it by hand once or twice with arguments to see what it returns.
- Put the taskmaster script in a convenient place -- probably your working subdirectory where you have the task.c source. If you execute the taskmaster script without arguments (be sure to set its executable bits) it will also tell you its argument list. If it complains about not knowing about threads, you will need to update your version of perl to one that includes thread support.
- Create a file named "hostfile" containing the names or IP numbers of the host(s) you wish to use in your parallel computation in the directory with taskmaster. I'd recommend having at least four participating hosts (one of which can be the "master" host that you are working from) but it would be great if you had as many as eight hosts in your NOW that you can put to work.
Task First, Cluster Later
Some of you who are reading this column to learn how to build clusters may be surprised (or even annoyed) that the focus this far is on parallel programming and not on what to do with wires and racks and super-fast dual central processing unit computers in custom cases and so forth. The hardware is what is interesting and cool -- racks of nodes and fancy networks and words like "supercomputer" and "teraflops". So why waste time on software?The reason is simple: engineering a successful cluster begins with understanding the nature of parallel software, not the hardware. The hardware is the easy part, in a sense; so easy that the NOW you have assembled (or discovered you already had without lifting a finger) is remarkably powerful and will likely yield good scaling behavior for many parallel tasks.
Ummm, about here you might ask (if you were a true neophyte): Just what is "good scaling behavior"? And while we are asking, which parallel tasks will yield it for this kind of cluster? Are there tasks that cannot be sensibly parallelized?
Actually, you'd ask these things only if you were really a bit advanced already. A true neophyte would be asking things like "can I read my mail faster on my 10 GFLOP NOW cluster?" (You laugh, but this question has appeared, with a variety of non-parallelizable applications taking the place of mail, over and over again on the Beowulf list beowulf (at) beowulf (dot) org. Or possibly you don't laugh, as this might be the very question that was in your mind! In case it isn't clear, the answer is
Only when we understand the answers to these questions will be able to address the much more difficult task of how to engineer a cluster that yields good scaling for tasks that would perform
In Foster's book, the stages of parallel program design are identified as partitioning, communication, agglomeration and mapping. In this article, we are exploring some of the consequences of various ways of partitioning a task deliberately designed to be completely parallelizable and running the resulting trivially parallelized program on a small cluster with fixed communications costs and a predetermined mapping of work to processors.
The term granularity is one you will often hear in a discussion of parallel computing. This is (in rough terms) the amount of work done in a single "chunk" of work resulting from a given task partitioning. If taskmaster's goal is to generate a list of random numbers, the finest grained partitioning of the task is just generating a random number (or set of random numbers) as a chunk of work, which isn't a lot of work at all and so the task is very fine grained in that limit. If instead taskmaster's goal is to simulate a long involved process whose final result is a number or set of numbers, the same task partitioning could be much coarser grained.
Task partitioning is a major parameter in the design of parallel programs; understanding it is equally important in the design of a parallel computer to run that program. Indeed, with a wide range of cluster and beowulf designs to draw upon, the parallel program design process can encompass both the program itself and the hardware to run the program on at the same time. This is the ideal towards which you should strive as you kickstart your cluster program, and it begins with the task.
where nhosts is the number of hosts to use (less than or equal to all of the hosts in hostfile), nrands is the number of random numbers you wish it to generate, and delay is the delay, in seconds, between each random number returned by each host.
With the list of ssh-accessible cluster nodes in hostfile, enter the following sequence of taskmaster jobs and record the return time for each. The example assumes that you have at least 8 hosts in hostfile; if not, use the biggest number of hosts you do have.
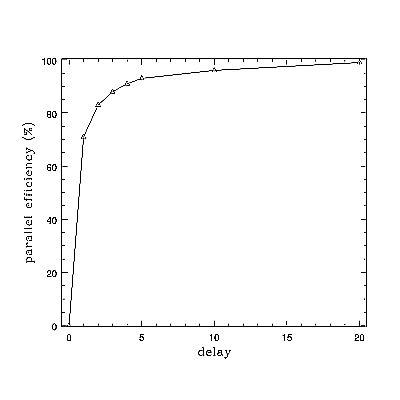
With an editor and a calculator compute and edit in the parallel efficiency = (nrands*delay)/(nhosts*time). A typical result might look like (also plotted in Figure One):
Let us understand this. We are generating 40 random numbers on 8 hosts,or five random numbers apiece. If delay is 0, it takes about 3 seconds just to start up the remote jobs and get back their (nearly instantaneous) replies with the results. However, it would take only 40*0 = 0 seconds (rounded) to generate all 40 on a single host, so efficiency is terrible.
If it takes 1 second per random number per host, the overhead of starting up and getting back the results actually goes down a bit, as the first hosts started up get to do some work while the rest of them start up and so less time is lost. It would take a single host 40 seconds to generate 40 rands (nrands*delay). A perfect speedup with 8 hosts would be 40/8 or 5 seconds total to generate our five rands. It takes us 7, so our efficiency is 5/7 or around 71%. And so on.
The important thing to learn from this is that as the work done to generate another rand (simulated by delay) increases relative to fixed overhead starting up the jobs and sending the rands back to taskmaster, the efficiency increases as well, approaching 100% as the work done takes much much longer than the startup and communication times! This is a scaling rule -- a rule that tells us what sort of parallel speedup to expect.
Let's extract and look at another. Following the general formula above and with calculator and editor in hand, use taskmaster and task to generate the following sequence of results:
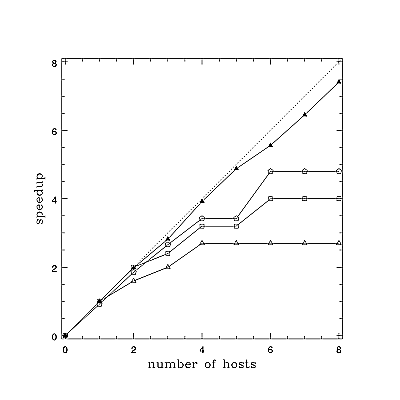
The results should look approximately like Figure Two, where [open triangles] are nrands=8, [open squares] are 16, [open pentagrams] are 24, and [filled triangles] are 40 with a delay of 5 instead of 1. The dashed line is perfect speedup - using N nodes makes the fixed size job complete in 1/N of the time, for an N-fold speedup.
Figure Two is a very informative figure. It illustrates many of the basic principles of cluster design and task scaling. From it we see that when a task is divided up among nodes in such a way that each node does a small amount of a small increment of work (compared to the overhead of task startup and communication) we may not speed up much as we increase the number of nodes allotted to the task. In the first three cases, we stopped speeding up altogether when between four and six nodes were assigned to the task (and have the uncomfortable, and correct, feeling that in the general case adding too many nodes could make the task slow down). However, we could assign more nodes to the task with some speedup resulting as we increased the amount of work being split up. Increasing the number of rands being generated helped some, but what really helped was increasing delay, the amount of "work" being done per rand. As we saw in Figure One, making delay large pushed the parallel speedup to one.
There are a few other important "knobs" that remain to be discovered. Some of these knobs are very much in hardware (for example, the speed of the network). Next month we'll tackle an important piece of algebra connected to a scaling relation known as Amdahl's Law. Using what we have learned so far, we'll derive an equation that describes the two figures above quite well (within the jigs and jags caused by using just a single sample with a fairly course time unit). With this equation in hand (and some measurements and thought) we can start to get a pretty good idea of the kind of performance we can expect from a given kind of cluster built for a given kind of problem -- before we spend all that money building the wrong kind (defined as one that wastes your money -and/or fails to get your work done).
This article was originally published in ClusterWorld Magazine. It
has been updated and formated for the web. If you want to read more
about HPC clusters and Linux, you may wish to visit
Linux Magazine.
Robert Brown, Ph.D, is has written extensively about Linux clusters. You can find his work and much more on his home page
Exploring Parallel Task Granularity
If you are getting or thinking about getting into the parallel/cluster computing game, at some point you are likely going to want to read a book on actual parallel program design. One such book that I can recommend is Ian Foster's Designing and Building Parallel Programs. One reason I can recommend it is because you can access it for free at until you decide that you'd like to own a paper copy (as I do) for easier reading and reference.
Taskmaster and its Task
With this as motivation, let us return to running taskmaster on our NOW.
The command syntax for taskmaster is:
taskmaster hostfile nhosts nrands delay
$ taskmaster hostfile 8 40 1 q > scaling.8
$ taskmaster hostfile 8 40 2 q >> scaling.8
$ taskmaster hostfile 8 40 3 q >> scaling.8
$ taskmaster hostfile 8 40 4 q >> scaling.8
$ taskmaster hostfile 8 40 5 q >> scaling.8
$ taskmaster hostfile 8 40 10 q >> scaling.8
$ taskmaster hostfile 8 40 20 q >> scaling.8
# nhosts nrands delay time parallel efficiency(%)
8 40 0 3 0
8 40 1 7 71
8 40 2 12 83
8 40 3 17 88
8 40 4 22 91
8 40 5 27 93
8 40 10 52 96
8 40 20 101 99
nhosts nrands delay time speed=nrands/time
0-8 8 1 ? ?
0-8 16 1 ? ?
0-8 24 1 ? ?
0-8 40 5 ? ?
Conclusion
Hopefully it is becoming apparent that cluster design requires a pretty good understanding of the scaling rules we observe in the figures above. Clearly we have identified a couple of "knobs" that can make a given cluster design more -- or less -- efficient, but they aren't in the hardware at all, they are in software! Or rather (no be more fair) they are linked to the hardware characteristics that determine things like the time required to complete an assigned work increment on a node. Still, if we had to summarize the results of today's exercises in a single phrase, it would be something like: coarse grained, gooood, fine grained, baaaaad. That's easy enough to remember.